Nu i morse blev jag intervjuad av Kristian Borglund som ansvarar för Metro Jobb. Han ville skriva en artikel om Tilf’s innovativa jobbannons som vi hade ute för några månader sedan när vi sökte en ny utvecklare. På torsdag kommer en fotograf till kontoret för att fotografera både mig och de två nya som anställdes.
Problemet som skulle lösas var följande
Ta ut F(n) mellan n=20 t.o.m. n=60 ur följande sekvens:
Om n är ett primtal spara det mittersta* talet ur F(n). Dessa mittersta tal resulterar i en talserie. Maila din ansökan till [svaret på talserien]@tilf.se
* = Exempel: Det mittersta talet i 1234 är 23. I 12345 är det mittersta talet 3.
Lösningen till problemet
Den som har läst någon slags programmeringskurs har säkert stött på ovanstående problem. Talserien kallas för Fibonacci talserien. Lösningsmetoderna var lika många som antalet ansökningar vi tog emot och kvalitén på ansökningarna var väldigt hög jämfört med vad man annars får in. Om man löst ovanstående uppgift korrekt så ska man få svaret 6426578921220 och man kunde då ansöka om jobbet.
Håll utkik i Metro den närmsta tiden för artikeln! =)
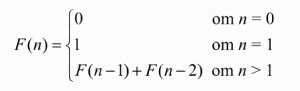

Jag lyckas inte få samma svar på denna räkneövning. De Fibonaccital i intervallet från F(20) till F(60) som är primtal är:
F(23) = 28657
F(29) = 514229
F(43) = 433494437
F(47) = 2971215073
Jag får svaret till 642921 !
(Nästa primtal i serien är
F(83) = 99194853094755497)
Hej Jan!
Kul att vårt lilla problem engagerar! =)
T.ex. är både 31 och 37 primtal. Sen finns det några till efter det. Försök vidare! =)
Beklagar, det var ju n, inte F(n) som skulle vara primtal, då blev ju problemet nästan trivialt.
Alltid skoj med såna här problem och gjorde först en snabb och enkel lösning men tyckte den var för långsam, så optimerade koden tills det tog ca 8 mikrosekunder att räkna ut det i C#.
Hur snabbt går det för andra lösningar?